In this article, I will discuss and summarize the paper: “Structural Analysis of Criminal Network and Predicting Hidden Links using Machine Learning” by Emrah Budur, Seungmin Lee and Vein S Kong.
Background
As in most criminal network projects, data is key. However, data is not always available, and if so, only in limited amount. Therefore, link prediction can make sense from that perspective. In this paper, authors gathered large amount of data and turned link prediction in graphs (which is a hard task) into binary classification problems (which is much easier).
Data
The authors gathered a dataset of 1.5 millions nodes worldwide with 4 millions undirected edges from the Office of Foreign Asset Control. I think that they refer to a dataset available here.
With such amount of data, the authors propose to turn a link prediction (predict links between times T and T+1), to finding hidden links by a binary classifier (at time T). There are several steps in the project:
- train a Gradient Boosting Model (supervised learning approach) on the current data for finding hidden links
- remove 5 to 50% of the edges to create a test set and compute the accuracy of the model
- distroy criminal networks using Weighted Pagerank index
To treat edge prediction as a classification problem, one should have features on each node and learn from them. The authors use as features:
- the number of common neighbors
- the jaccard index
- the preferential attachment index
- the hub index
- the Adamic/Adar index
- the Leicht Holme index
- the Salton index
- the Sorensen index
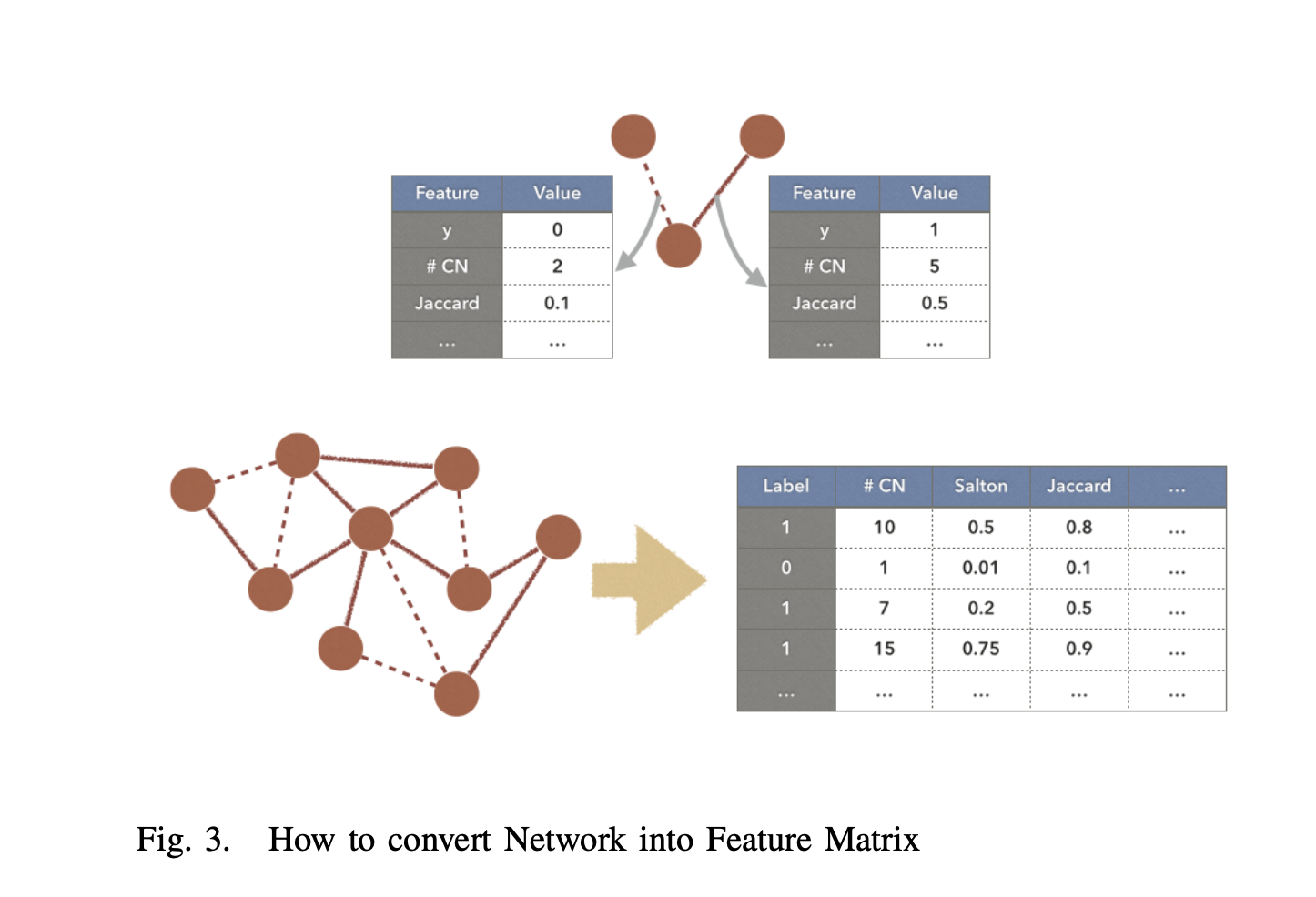
They build a training dataset (75%), and a test one in which they remove edges. To build the feature matrix, they compute combinations between all possible nodes. Therefore, they end up with more negative edges (\(E_{-}\)) than positive edges (\(E_{+}\)). To balance the training set, they apply a random undersampling on the negative edges.
Model and performance
The metric chosen is the prediction imbalance:
\[Pred_{Imbalance} = \mid err_{+} − err_{-} \mid\]The authors also compute the Area under the curve (AUC) criteria. They gradually remove from 5% up to 50% of the edges, and the findings are quite interesting:
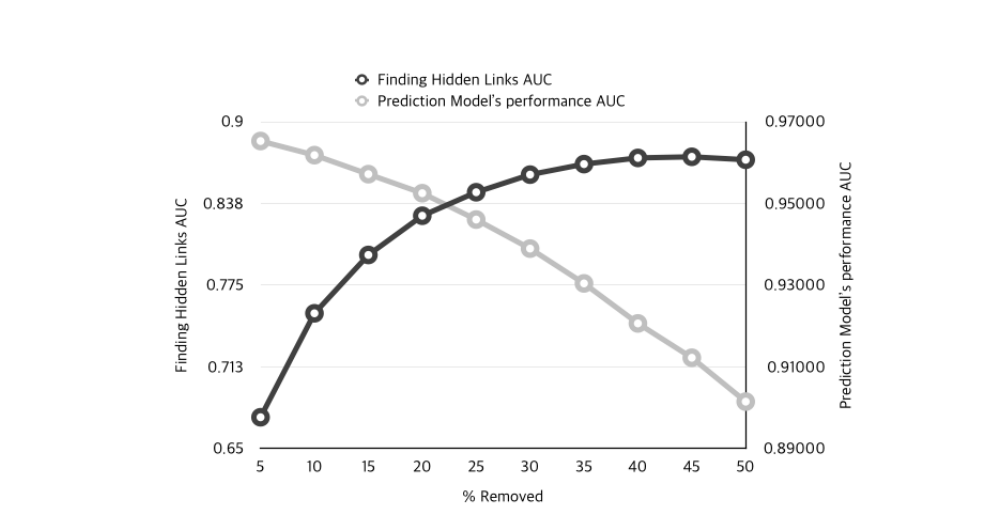
The light gray line shows the performance of the model when we build a train and a test set from a corrupted network. The more edges were removed before splitting in \(D_{train}\) and \(D_{test}\), the lower the model performance.
The dark line is the ability of the built model to find hidden links. And surprisingly, AUC increases with the proportion of links removed. Authors argue that it comes from the fact that the model might overfit on the structure of the graph when given too many links in training, and that removing some edges during training (typically anywhere close to 25-30%) could improve the model.
Destroying networks
In the paper “Disrupting Resilient criminal networks through data analysis”, authors identify the nodes with the highest betweenness centrality and remove them gradually in order to disrupt the network.
In this paper, authors argue that removing nodes with the highest pagerank score first improved the disruption of the network.
The data does not provide weights on edges. These weights are added by making the model predict the existing edges. A score closer to 1 will give a weight closer to 1, and a score closer to 0 will give a weight closer to 0.
Weighted pagerank scores are then computed in the network, for each node. The index computed by the pagerank algorithm builds a “suspiciousness index”, and more suspicious nodes should be removed first. The authors compared several node removal strategies (Unweighted pagerank, weighted pagerank, node degree, jaccard index…).
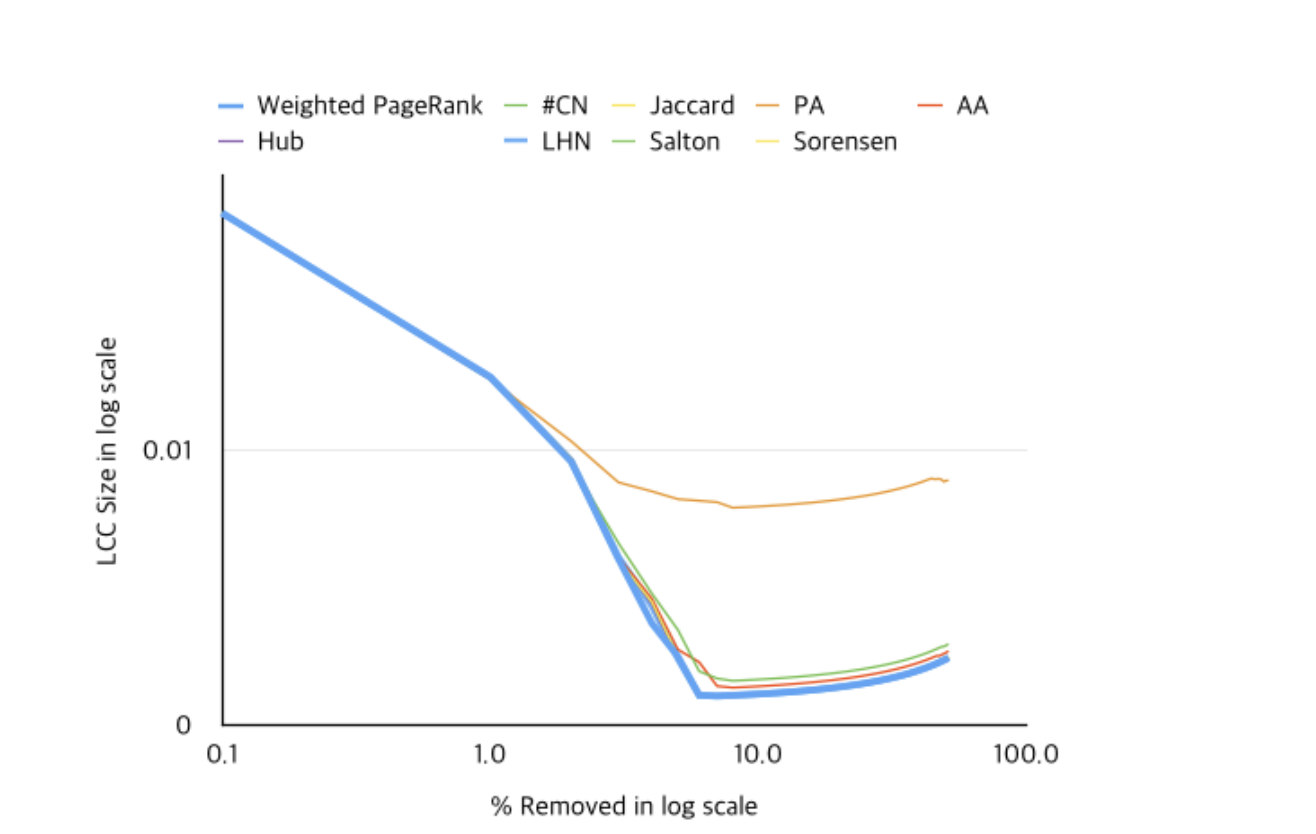
The removal of nodes having maximum Weighted PageRank score reduces the largest connected component (LCC) of the network much faster than removal of nodes based on any other metric, except for unweighted pagerank (no clear difference).
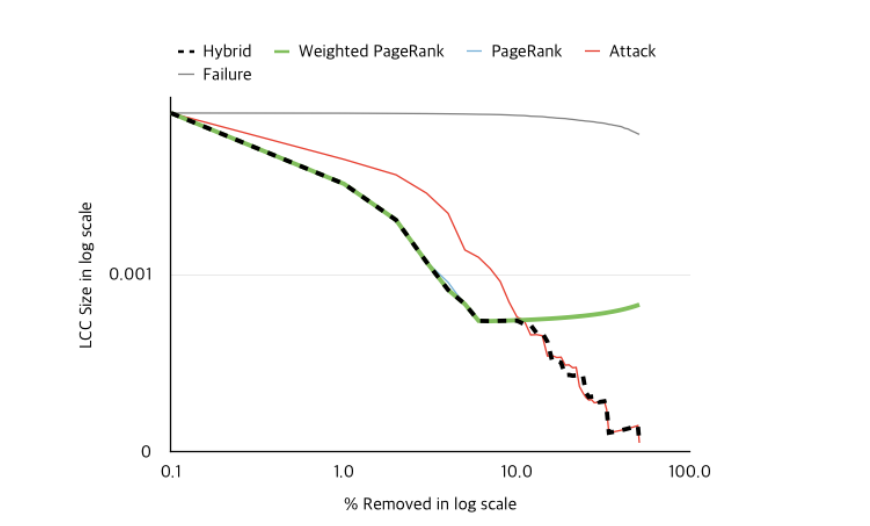
All pagerank methods reach a bottleneck after some time, since the pagerank is computed only once, and not after each iteration. Therefore, 2 options:
- re-compute pagerank at each step, which can get quite expensive in terms of computation
- use the hybrid method proposed by the authors to maximize the WCC score: parameters \(W_{hybrid} ≈ min(W_{Weighted Pagerank}, W_{Attack})\)
The first approach was not implemented by authors, but the second one seems to improve the percentage of the network removed where the pagerank reached a bottleneck.
Discussion
The work discussed in this paper is quite interesting by the volume of the data considered. A supervised machine learning model could be trained, and undersampling seemed to help. One should try other models and other features in future works.
The dataset, although massive, lacks the notion of weights and does not have a temporal notion, it’s only a snapshot.
