Modéliser la distribution de données avec Python (Distribution Fitting)

Cet article suppose une connaissance préalable des lois de probabilités les plus communes.

Modéliser une distribution

La modélisation de la distribution de données (probability distribution fitting, ou distribution fitting en anglais) est le fait de trouver les paramètres de la loi de distribution de probabilité (ou de plusieurs lois candidates) qui correspond aux données que l’on cherche à modéliser.

En d’autres termes, on souhaite savoir si nos données suivent par exemple une loi normale, une loi gamma, ou toute autre distribution, et les paramètres attachés à la loi.

Pourquoi cherche-t-on à modéliser la distribution de nos données? L’information qu’apporte la distribution de nos données est en fait essentielle. Cela nous permet notamment déterminer la fréquence d’occurrence d’un certain phénomène. C’est une information très utilisée par les actuaires dans le monde de l’assurance afin de déterminer la probabilité qu’une perte dépasse un certain montant par exemple. Cette information est également utilisée en analyse de risque, en économie ou dans des études de fiabilité en ingénierie.

La modélisation de la distribution de données est souvent utilisée dans les logiciels d’exploration de données, car elle permet de comprendre les propriétés sous-jacentes de nos données.

La modélisation de la distribution de données est une tâche qui peut s’effectuer de deux manières:

• Manuellement. Vous avez une idée de la loi de distribution, ou de quelques lois candidates. Pour chaque loi, vous trouvez les paramètres optimaux par maximum de vraisemblance (ou Maximum Likelihood Estimation, MLE en anglais), ou par la méthode des moments (Method of Moments) par exemple.
• Automatiquement. Vous utilisez une librairie ou un logiciel spécialisé, qui a déjà implémenté les maximums de vraisemblance de nombreuses lois, et cherchez à trouver la meilleure loi et les meilleurs paramètres d’un coup.

Implémentation et exemple

Supposons que vous travaillez dans une assurance, et disposez d’une série de données qui correspond aux montants des remboursements que l’assurance a effectué pour les différents assurés de son portefeuille “Assurance Voiture”. En clair, dès qu’un client qui est assuré chez vous a un accident avec son véhicule, le montant que vous lui remboursez est rentré dans la série de données. Il y aura typiquement beaucoup de paiements d’un petit montant, et quelques paiements d’un montant élevé. Cependant, on peut aussi s’attendre à ce que les plus petits montants ne soient pas déclarés par les assurés, car cela peut impacter leur bonus pour les années suivantes. Si l’on représente l’histogramme des données, voici ce à quoi on peut s’attendre:

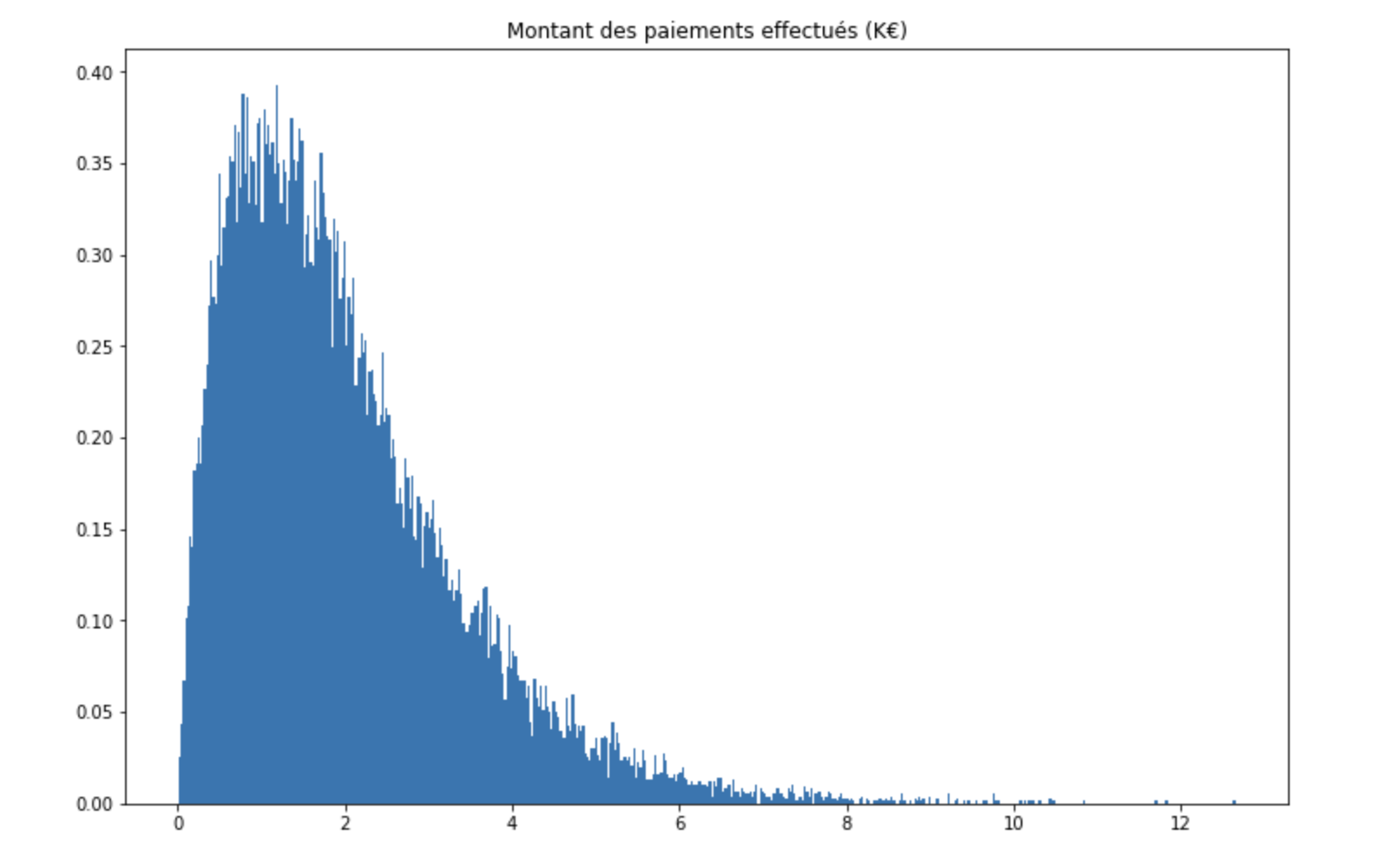
On observe que:

• pour des montants très faibles (<500€), les demandes de paiement sont faibles
• un pic est atteint pour des montants avoisinnant les 1’000€
• plus le montant augmente, moins il y a des cas de sinistres enregistrés

Modélisation d’une distribution connue

Avec Python, il est simple de réaliser une modélisation automatique de la distribution de nos données. C’est ce que nous allons voir maintenant! Tout d’abord, importez les librairies suivantes:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy
import scipy.stats
import time

Nous allons ensuite simuler de fausses données d’un portefeuille d’assurance. Nous allons générer des données suivant une loi Gamma.

# Nombre de valeurs à générer
length = 30000
bins=500

# Génération des données
data = np.random.gamma(2,1, length)

# Histogramme des données
y, x = np.histogram(data, bins=bins, density=True)
# Milieu de chaque classe
x = (x + np.roll(x, -1))[:-1] / 2.0

On peut alors représenter visuellement un histogramme données:

plt.figure(figsize=(12,8))
plt.hist(data, bins=500, density=True)
plt.title("Montant des paiements effectués (K€)")
plt.show()

Afin d’identifier, pour une loi de distribution donnée, les paramètres correspondant au maximum de vraisemblance, nous allons utiliser la librairie scipy, qui offre près de 80 distributions dans sa version actuelle, et identifie les paramètres optimaux par maximum de vraisemblance.

Il suffit de spécifier la loi que l’on souhaite tester, et d’utiliser la méthode fit de Scipy pour récupérer les paramètres optimaux. Par exemple:

dist_name = "gamma"

# Paramètres de la loi
dist = getattr(scipy.stats, dist_name)

# Modéliser la loi
param = dist.fit(data)

La variable param contient alors:

(1.993299446023943, -0.0005280086059209502, 0.9929125608037362)

Les paramètres correspondent à:

• shape : 1.9933, contre une vraie valeur de 2
• loc : -0.0005, contre une vraie valeur de 0
• scale : 0.9929, contre une vraie valeur de 1

On peut alors re-tracer la distribution de probabilité de la loi Gamma avec ces paramètres.

loc = param[-2]
scale = param[-1]
arg = param[:-2]

pdf = dist.pdf(x, loc=loc, scale=scale, *arg)

plt.figure(figsize=(12,8))
plt.plot(x, pdf, label=dist_name, linewidth=3) 
plt.plot(x, y, alpha=0.6)
plt.legend()
plt.show()

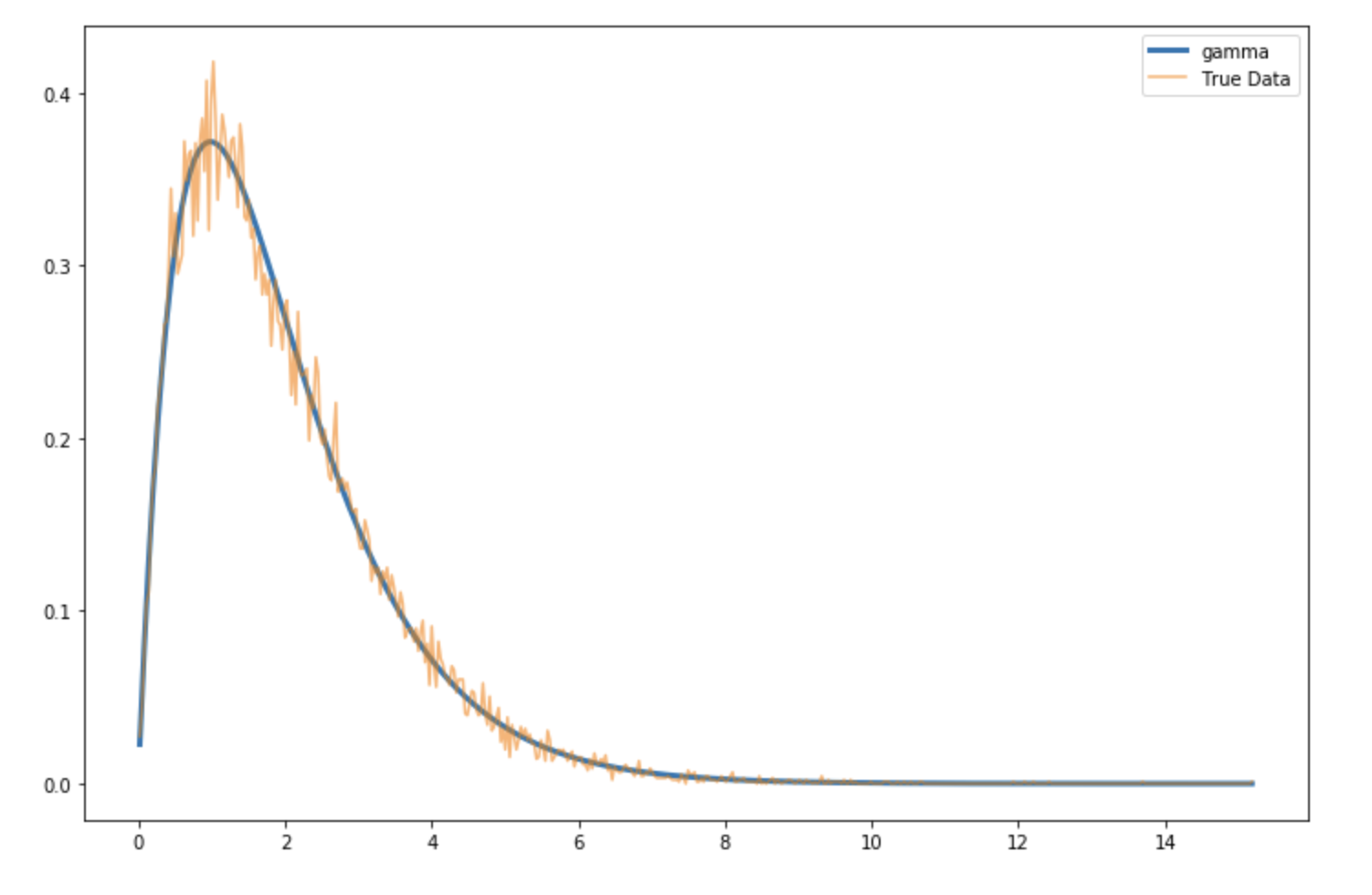
La PDF (probability distribution function), ou densité, de la loi Gamma avec les paramètres identifiés par Scipy est très proche des données originales. Comment peut-on cependant mesurer la distance entre les deux courbes? Il existe plusieurs mesures de distance, mais une des plus populaires est la somme de résidus au carrés (sum of squared errors, en anglais). On peut calculer la somme des résidus au carré de cette manière:

sse = np.sum((y - pdf)**2)

Ici, la somme des résidus au carré vaut 0.04362. Ce chiffre nous permettra de sélectionner la meilleure loi lors que nous testerons plusieurs lois à la fois. En effet, jusque-là, nous avons simplement généré des données selon une loi gamma, puis identifié les paramètres par maximum de vraisemblance pour cette même loi.

Plusieurs lois candidates

Afin d’identifier la meilleure loi, il suffit de répéter le processus opéré jusque-là, mais pour toutes les lois que nous souhaitons tester. Dans un premier temps, on définit dans une liste l’ensemble des lois à tester:

dist_names = ['norm', 'beta','gamma', 'pareto', 't', 'lognorm', 'invgamma', 'invgauss',  'loggamma', 'alpha', 'chi', 'chi2']

Ces lois correspondent globalement aux lois les plus communes, implémentées dans scipy. Par la suite, nous pouvons itérer afin de modéliser la distribution de nos données pour chacune de ces lois. Nous allons définir un seuil de la somme des résidus au carré en dessous duquel nous acceptons une loi comme une bonne candidate. Cela nous permet alors de réduire le temps de calcul, et de s’arrêter dès qu’une candidate satisfaisante est identifiée.

sse = np.inf
sse_thr = 0.10

# Pour chaque distribution
for name in dist_names:

	# Modéliser
	dist = getattr(scipy.stats, name)
	param = dist.fit(data)

	# Paramètres
	loc = param[-2]
	scale = param[-1]
	arg = param[:-2]

	# PDF
	pdf = dist.pdf(x, *arg, loc=loc, scale=scale)
	# SSE
	model_sse = np.sum((y - pdf)**2)

	# Si le SSE est ddiminué, enregistrer la loi
	if model_sse < sse :
		best_pdf = pdf
		sse = model_sse
		best_loc = loc
		best_scale = scale
		best_arg = arg
		best_name = name

	# Si en dessous du seuil, quitter la boucle
	if model_sse < sse_thr :
		break

Ensuite, on affiche la loi sélectionnée, les paramètres identifiés et on représente le tout graphiquement.

plt.figure(figsize=(12,8))
plt.plot(x, y, label="Données")
plt.plot(x, best_pdf, label=best_name, linewidth=3)
plt.legend(loc='upper right')
plt.show()

# Détails sur la loi sélectionnée
print("Selected Model : ", best_name)
print("Loc. param. : ", best_loc)
print("Scale param. : ", best_scale)
print("Other arguments : ", best_arg)
print("SSE : ", sse)

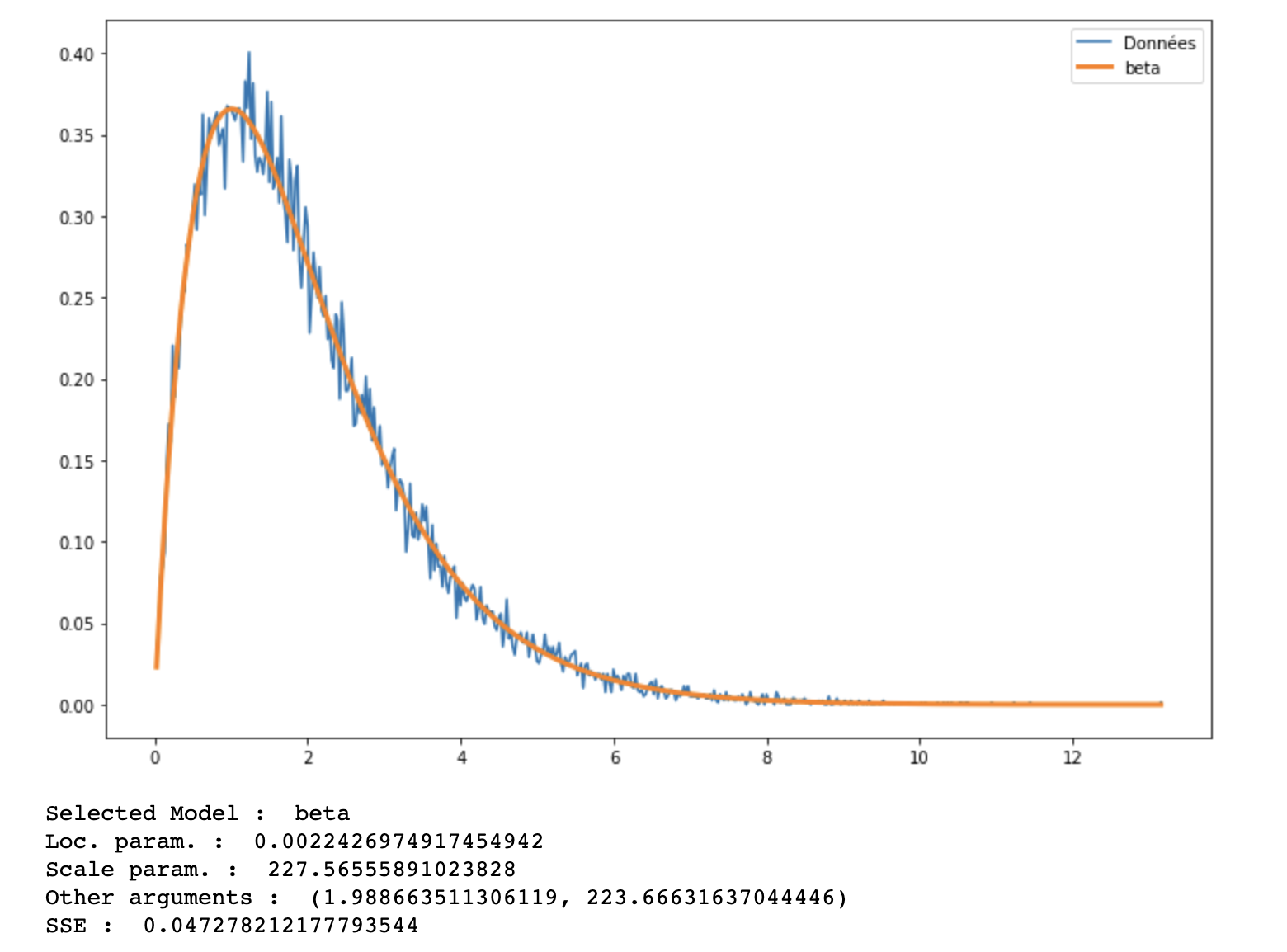
Ici, la loi Beta est identifiée comme meilleure candidate en 3.17 secondes, car on passe par cette loi dans la boucle avant la loi Gamma et qu’elle satisfait le critère du seuil de la somme des résidus au carré. Si on descend le seuil à 0, la loi identiée est une loi Gamma. Notre exemple reste simpliste car les données à modéliser sont générées à partir d’une des lois candidates. Que se passe-t’il si l’on vient perturber ces données avec un bruit gaussien?

y = y + np.random.randn(bins)/50

En perturbant y et en ré-exécutant le code ci-dessus, la loi identifiée est une loi Gamma. La loi Beta ne satisfait plus, dans cet exemple, le critère du seuil de la somme des résidus au carré.

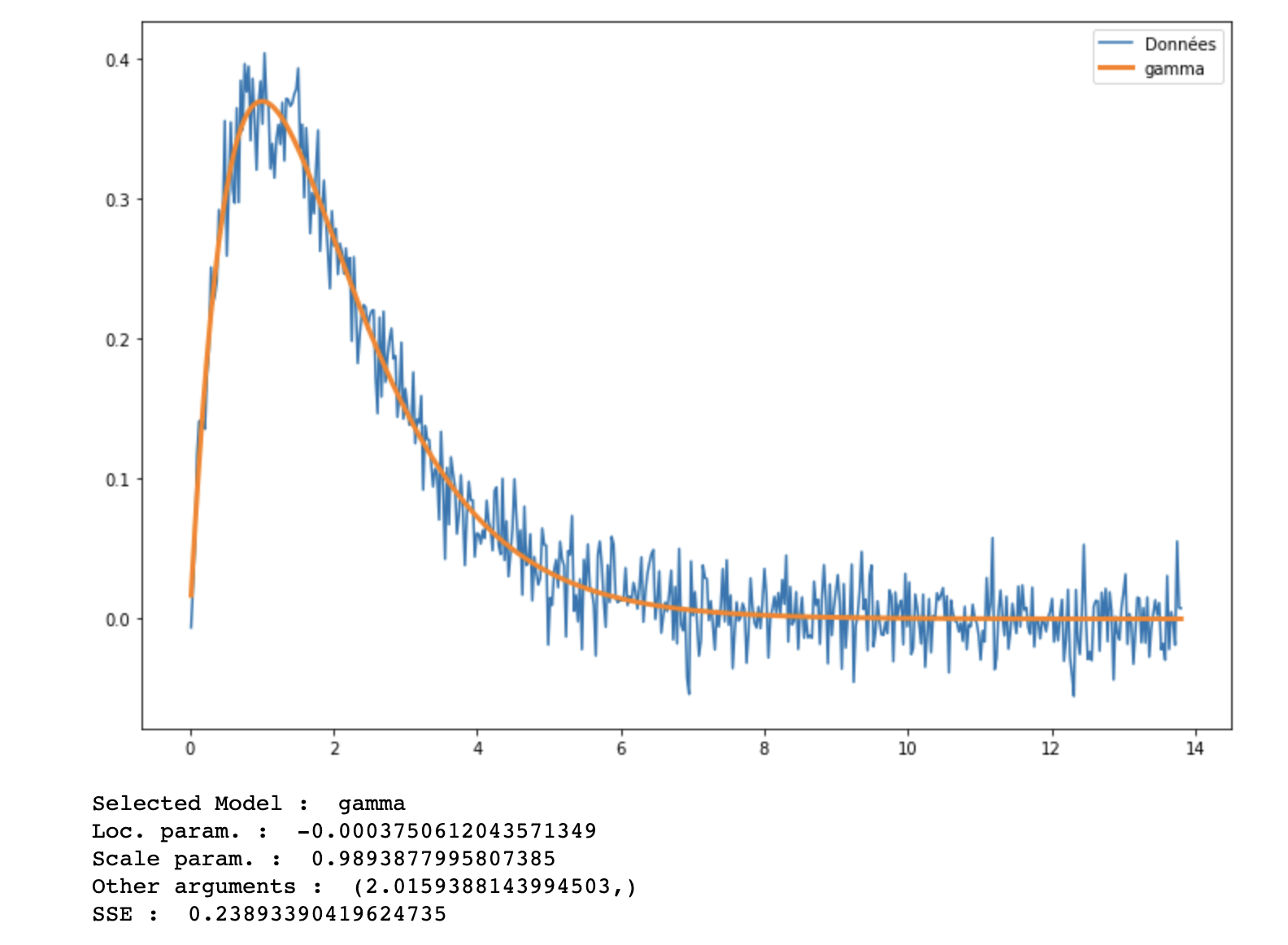
Application Web Interactive

Afin de comprendre l’influence du seuil défini, des paramètres de départ de la loi générée ou de la perturbation gaussienne, il est intéressant de mettre en place une application web interactive. C’est ce que nous allons faire avec Streamlit! Streamlit est un nouveau service qui permet de déployer des applications et des modèles entrainés en quelques linges de code seulement.

Voici une démonstration de l’application:

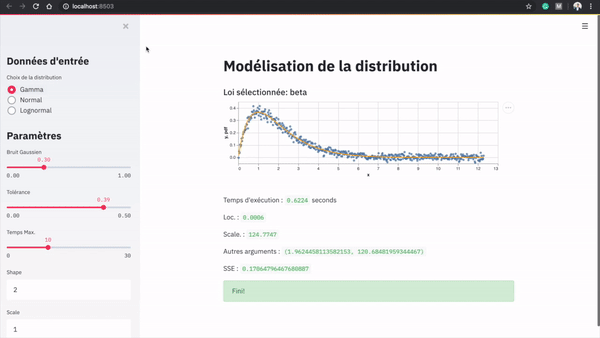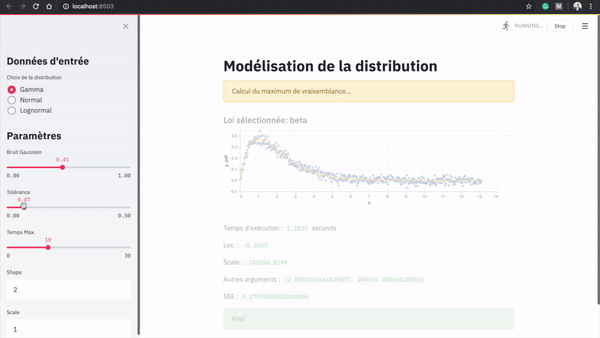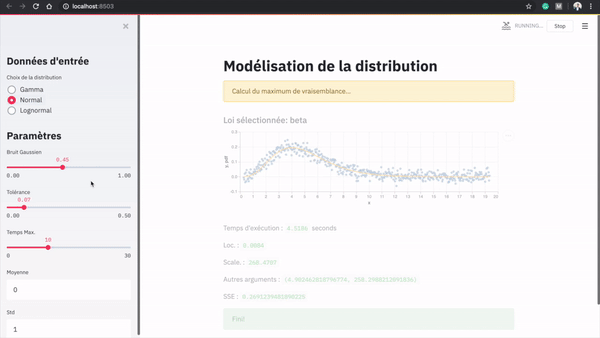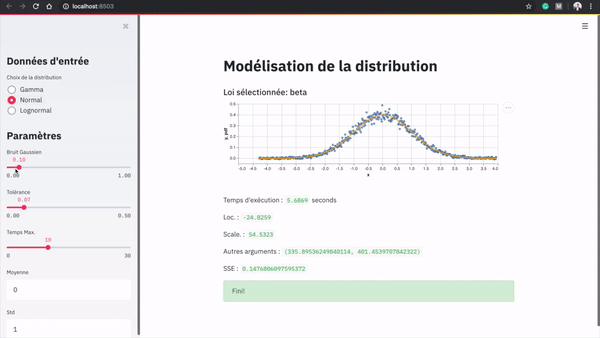
Dans le menu latéral, l’utilisateur peut générer des données selon une loi initiale. Il peut décider des paramètres de la loi qui sert à générer les données et d’une perturbation à ajouter. Il peut ensuite ajouter une tolérance en termes de somme des résidus au carré, et allouer un budget de temps pour l’algorithme de modélisation.

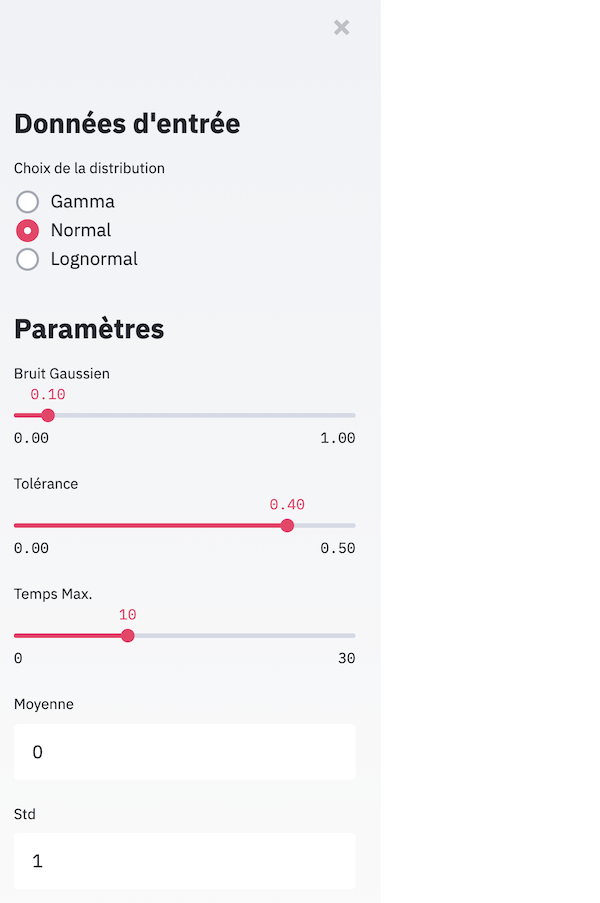
Les données sont ensuite générées automatiquement et l’algorithme de modélisation est lancé. La meilleure loi identifiée, les paramètres et le temps d’exécution sont alors affichés.

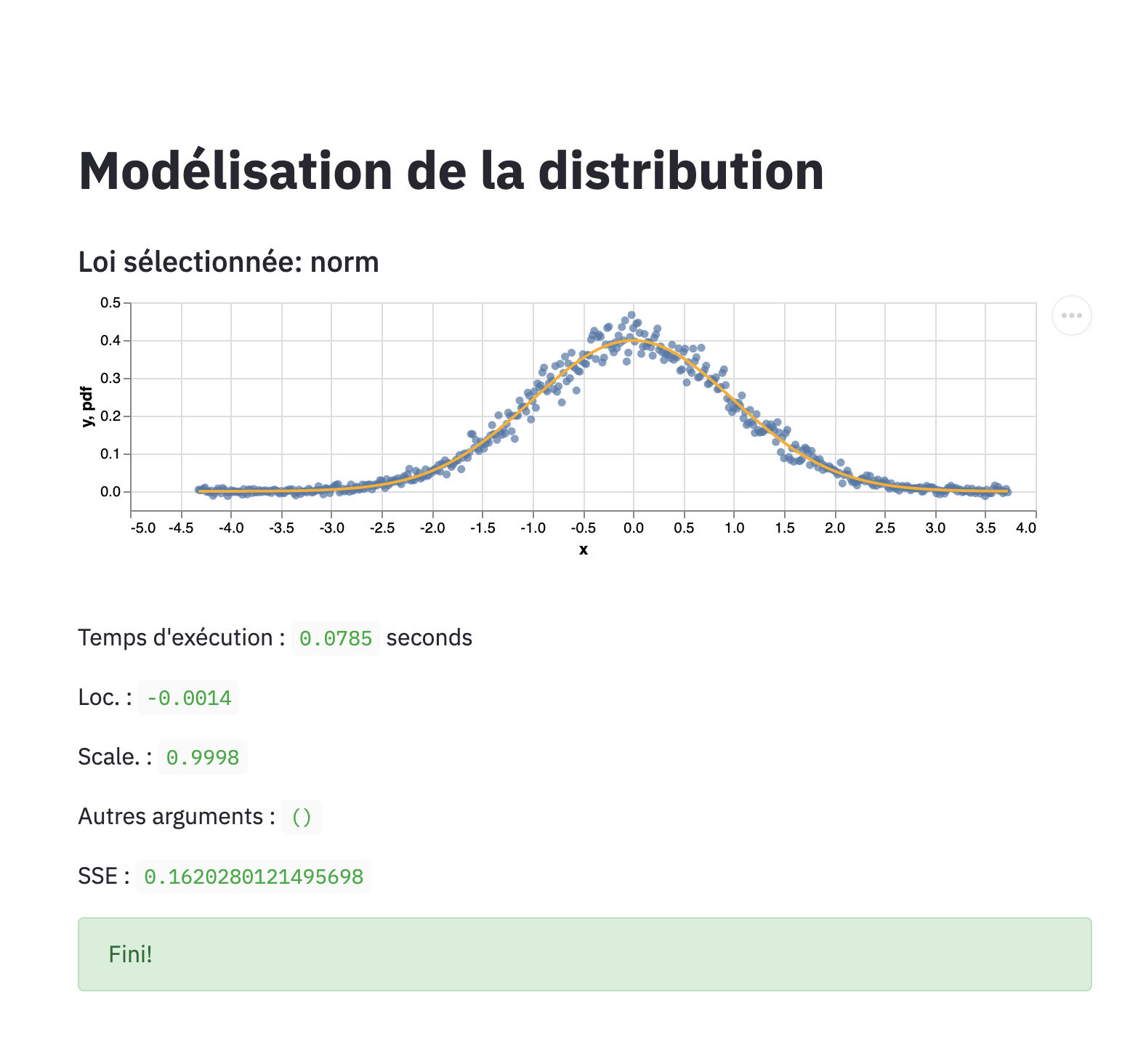
Pour installer Streamlit, il suffit de passer par pip:

pip install streamlit

Le code de l’application Streamlit est disponible sur Github. Pour lancer l’application Streamlit en local, il suffit d’exécuter la commande suivante:

streamlit run dist.py

Conclusion

A travers cet article, nous avons identifié les enjeux de la modélisation de distribution, et présenté une méthode automatisée pour identifier la loi optimale et les meilleurs paramètres par maximum de vraisemblance. Avec l’appui d’applications interactives comme Streamlit, l’exploration des différents scénarios de modélisation est bien plus intéractive.