Convolutional Neural Networks

Convolutional Neural Networks (CNN) are feed-forward neural networks that are mostly used for computer vision or time series analysis. They offer an automated image pre-treatment as well as a dense neural network part. CNNs are special types of neural networks for processing data with grid-like topology. The architecture of CNNs is inspired by the visual cortex of animals.

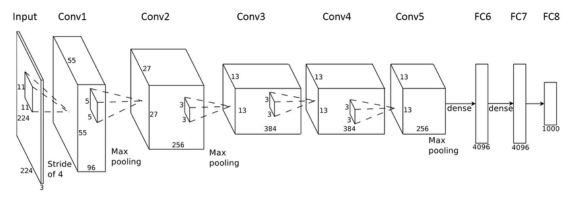
What is a CNN?

Filters

The main idea behind using CNNs is to extract more information than the pixel value itself. Indeed, individual pixel values do not bring a lot of information. For this reason, we apply filters on the images. Historically, a great part of the work was to select these filters manually (e.g Gabor filters) and architecture of the filters to extract as much information from the image as possible. The aim of these filters was for example to extract :

• edges
• contrast zones
• dark or light zones
• …

How can we extract information from a filter? Well, you should see a filter as a sliding window that creates an operation locally, between all the pixels located in a region.

Therefore, we can extract more information than a single pixel value. If you’re interested in this, check my articles on computer vision and filtering. Here is an example with some values in a matrix :

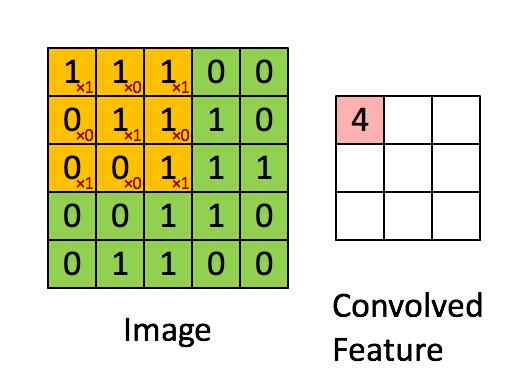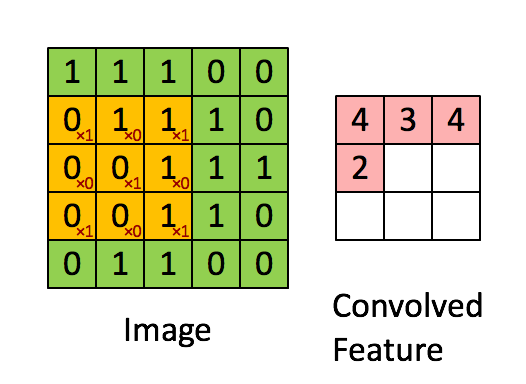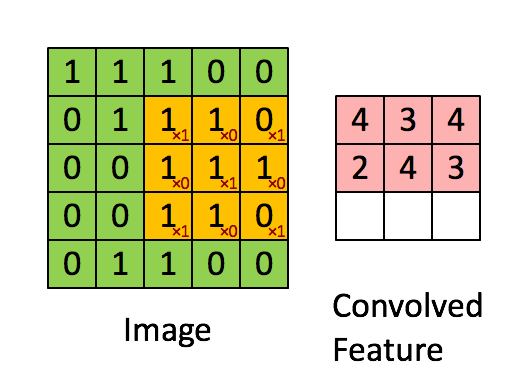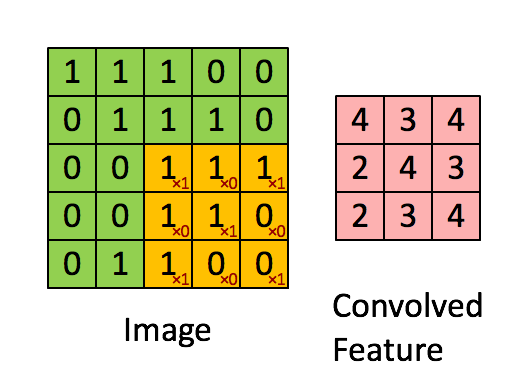
Automatic image processing

With the rise of deep learning and greater computation capacities, this work can now be automated. The name of the Convolutional Neural Networks comes from the fact that we convolve the initial image input with a set of filters. This time, we don’t have to select the filters anymore. The parameter to choose to remain :

• the number of filters to apply,
• the dimension of the filters
• the step size with which we convolve the filter with the image
• the padding

The dimension of the filter is called the kernel size. Typical values for the stride lie between 2 and 5. For example, on an image of size \(100 \times 100\), we can apply a filter of size 5.

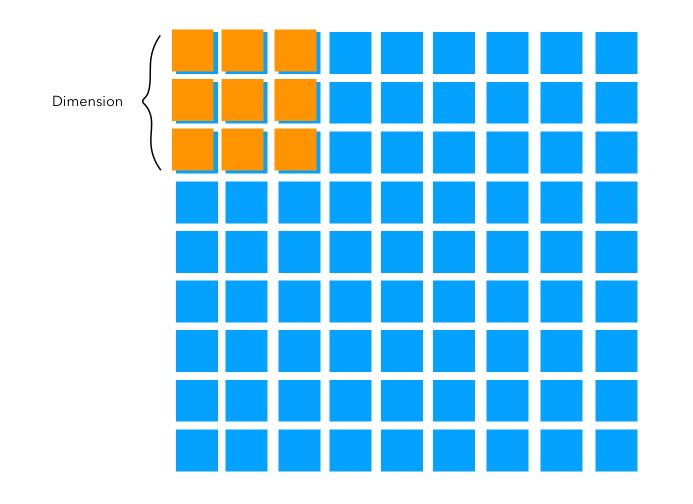
The step size is simply the amount by which we shift the filter at each step.

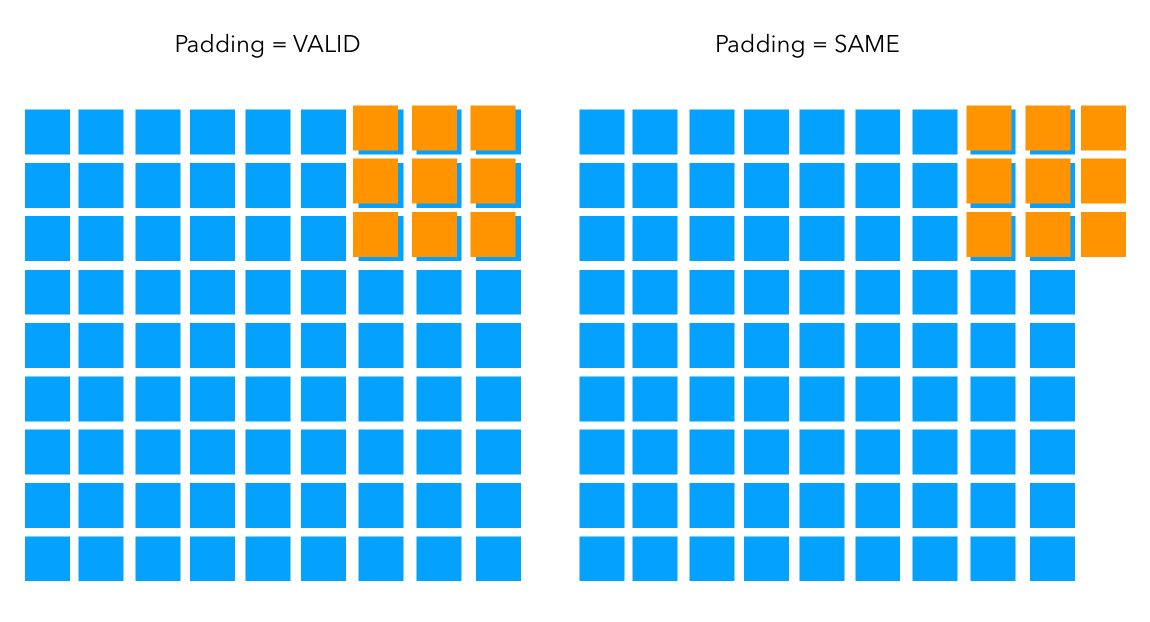
When we convolve a filter with an image, we’ll reach the end of the row of pixels at some point. There are two approaches in this case :

• either we stop when the extremity of the filter reaches the boundary of the image. This is called: padding='valid' in Keras for example. In this case, we lose a bit of the dimension of the image.
• otherwise, we convolve the image to keep the original dimension. This is called: padding='same' in Keras. Filter window stays at valid position inside input map.

By adding several filters, we convolve the image with filters many times. In some sense, we are building a convolved output that has a volume. It’s no longer a 2-dimensional picture. The filters end up being hardly humanly understandable, especially when we use a lot of them. Some are used to find curves, other edges, other textures…

A bit of maths

Convolution layer

Mathematically, the convolution is expressed as such : \((f * g)(t) = f(t) * g(t) = \int_{-\infty}^{+\infty} f(\tau)g(t-\tau) \partial \tau\)

The convolution represents the percentage of area of the filter (g) that overlaps with the input \(f\) at time \(\tau\) over all time \(t\) . However, since \(\tau < 0\) and \(\tau > t\) have no meaning, the convolution is described as :

\[(f * g)(t) = \int_{0}^{t} f(\tau)g(t-\tau) \partial \tau\]

In the discrete case :

\[f[t] * g[t] = \sum_{-\infty}^{+\infty} f[k] g[t-k]\]

If we have a function of 2 variables, in the continuous case :

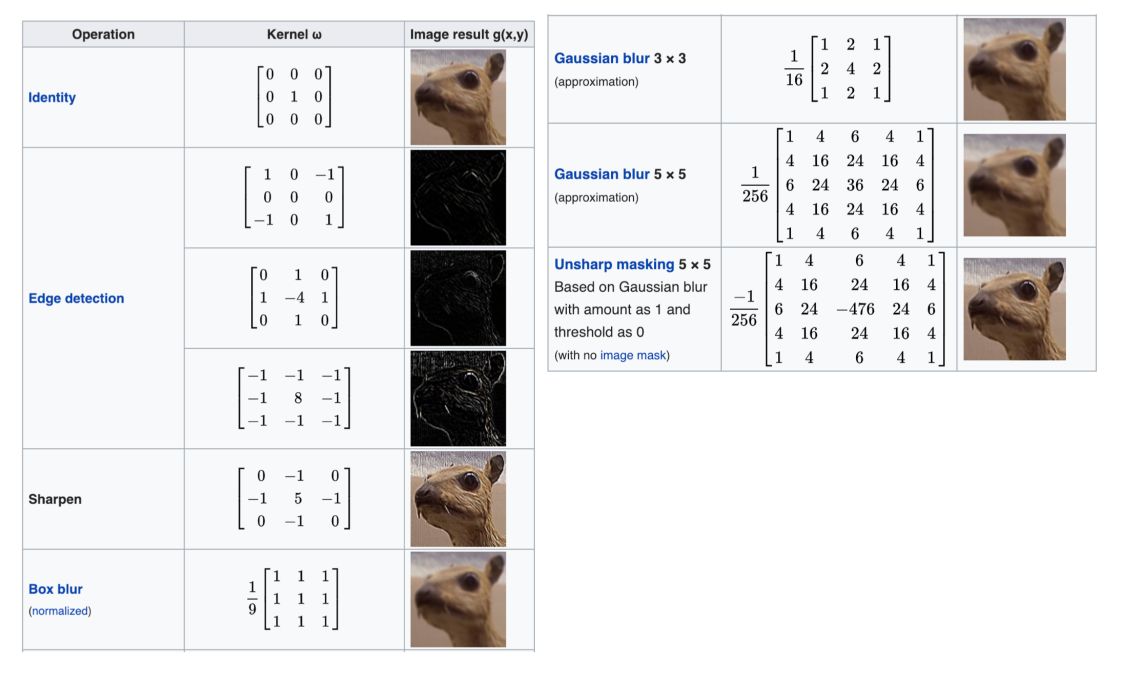
\[f(x,y) * g(x,y) = \int_{\tau_1 = -\infty}^{+\infty} \int_{\tau_2 = -\infty}^{+\infty} f(\tau_1, \tau_2) * g(x-\tau_1, y-\tau_2) \partial \tau_1 \partial \tau_2\]

What kind of filters are usually applied? Wikipedia brings a clear illustration of this :

Activation function

At each convolution step, for each input, we apply an activation function (usually ReLU). So far, we have only added dimensionality to our initial image input. The activation function brings non-linearity in a neural network. Otherwise, a neural network would be simply a linear function. There are many types of activation function. The most common ones to apply on the hidden layers are the following :

• ReLU (Rectified Linear Unit) : \(f(x) = max(0,x)\)
• Leaky-ReLU : \(f(x) = 0.001*x\) if x < 0, \(x\) else.

There are other activation functions that we use on the final layer :

• Softmax : If your output is a one-hot matrix, you might want to transform the output into probabilities for each class. The softmax function is defined as \(f(x_i) = \frac {e^{x_i}} { \sum_i {e^{x_i}}}\)
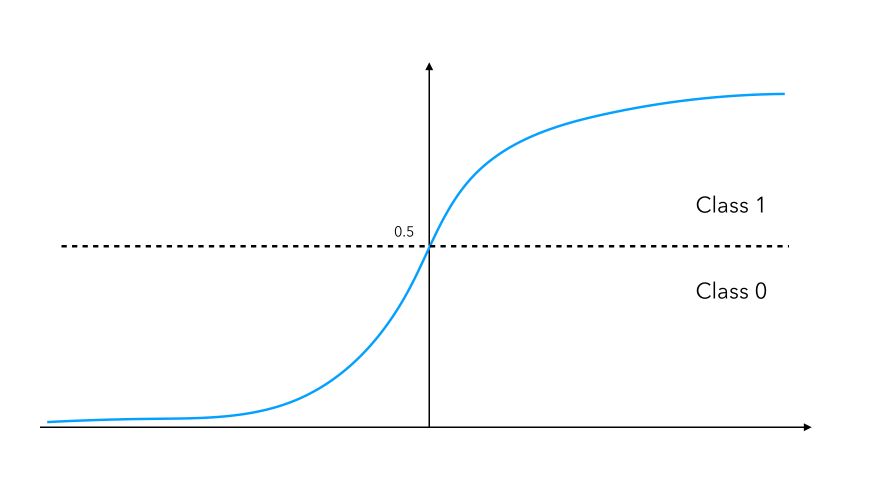
• Sigmoid : If you face a binary classification task, you’ll have a single output neuron, and using a sigmoid activation will assign the value of either 0 or 1 to your output. The sigmoid function is defined by : \(f(x) = \frac {1} {1 + e^{-u}}\)

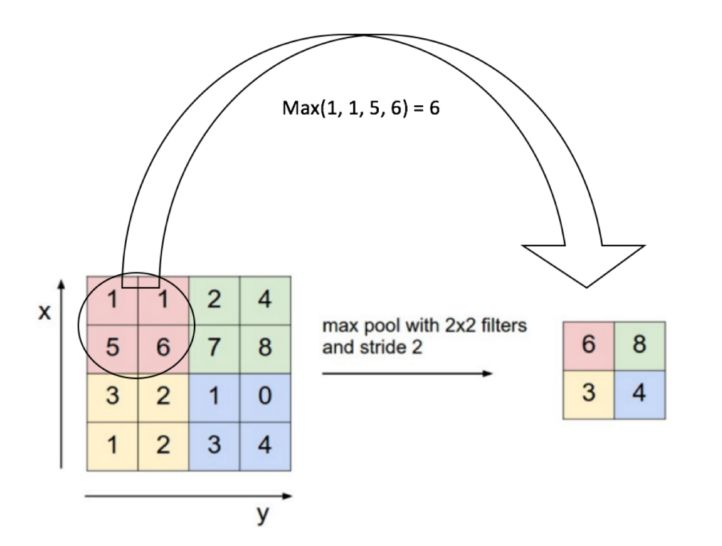
Pooling

We then apply a so-called pooling. Pooling involves downsampling of features so that we need to learn fewer parameters when training. The most common form of pooling is max-pooling. For each of the dimension of each of the input image, we perform a max-pooling that takes, over a given height and width, typically 2x2, the maximum value among the 4 pixels.

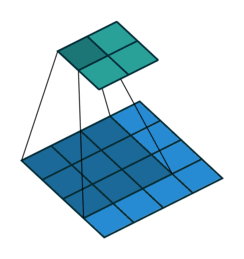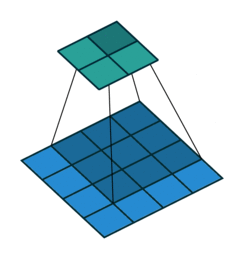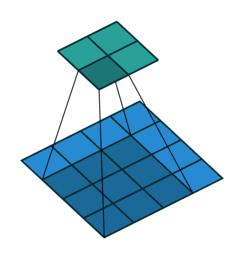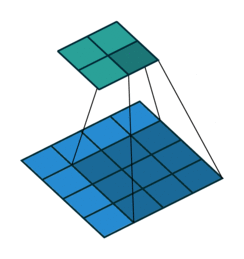
The intuition is that the maximal value has higher chances to be more significant when classifying an image.

We have now covered all the ingredients of a convolution neural network :

• the convolution layer
• the activation
• the pooling layer
• the fully connected layer, similar to a dense neural network

The order of the layers can be switched :

\[ReLU(MaxPool(Conv(X))) = MaxPool(ReLU(Conv(X)))\]

In image classification, we usually add several layers of convolution and pooling. This allows us to model more complex structures. Most of the model tuning in deep learning is to determine the optimal model structure. Some famous algorithms developed by Microsoft or Google reach a depth of more than 150 hidden layers.

I’ll make another article in which I’ll cover the maths behind deep learning if you’re interested.

Implementing CNNs in Keras

Implementing a CNN in Keras can be done the following way. Start by importing the following package :

from keras.models import Sequential
from keras.layers import Dense, Conv2D, Flatten, Activation, Dropout, MaxPooling2D
from keras.layers.normalization import BatchNormalization
import numpy as np

Say that our aim here is to make a binary classification from input images of size \(100 \times 100\). It could be a classification of the gender of the person for example. We want to use a sigmoid activation function on the neuron output.

We can then build the model in Keras :

#create model
model = Sequential()

#add model layers
model.add(Conv2D(512, kernel_size = (3,3), input_shape=(100,100,1)))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(3, 3)))
model.add(Dropout(0.1))

model.add(Conv2D(256, kernel_size = (3,3)))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(3, 3)))
model.add(Dropout(0.1))

model.add(Conv2D(128, kernel_size = (3,3)))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(MaxPooling2D(pool_size=(3, 3)))
model.add(Dropout(0.1))

model.add(Flatten())

model.add(Dense(1, activation='sigmoid'))

As you can see, we add several convolutions, max pooling, and batch normalization layers, before flattening the output of the layers and adding several dense layers. The final dense layer here contains the number of classes we are working within the inputs.

You can print the summary of the model the following way :

model.summary()

To compile and fit the model, simply run :

model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X, y, batch_size=128, epochs=10000, validation_split = 0.2)

You can choose :

• the optimizer (we tend to use Adam most often)
• the loss (here, binary cross-entropy)
• the metric to use (our problem is balanced, so accuracy is just fine)
• the training data and the validation split (if you have validation data, you can use them with validation_data = (X_val, y_val))
• the batch size, i.e. the number of training samples you use per batch
• the number of epochs for the training

**Conclusion **: CNNs are nowadays key elements in computer vision. If you have a question, don’t hesitate to comment on the article.